Our first challenge, in Activity 1, was to measure all angles in a set of pattern blocks using nothing more than this:
My normally brilliant student looked at me like I had lost my mind. How in the world could you measure the angles of a pattern block with that??? We first talked about what we knew:
1. Straight line = 180 degrees
2. Perpendicular line = 90 degrees
3. Orange square pattern block has to have 90 degree angles because it's a square. It also fits in the corner of the drawing above.
But what about all the rest of the shapes? How could you figure their angles?
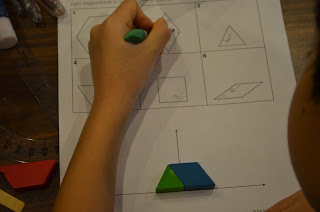
After a time, we discovered that pattern blocks could be combined to form a straight angle of 180 degrees. In the example below, we could see that 3 triangles (or in the illustration, 1 triangle + 1 rhombus) formed a straight angle. Therefore, 180/3 = 60 degrees...or 1 green triangle has angles of 60 degrees each since it's an equilateral triangle. In a similar fashion, we made combinations of pattern blocks until we knew the angles of all the pattern blocks. Pattern blocks now became a tool for additional measurement opportunities.
 In Activity 2, we measured "Human Angles," first considering real-world connections: a sister who had to have physical therapy for a knee injury, a brother whose extreme joint mobility allows him to do circus-like feats of movement,...even a non-human connection--an owl--and it's circular head movement. But at first it wasn't easy for us to see human movement in degrees.
In Activity 2, we measured "Human Angles," first considering real-world connections: a sister who had to have physical therapy for a knee injury, a brother whose extreme joint mobility allows him to do circus-like feats of movement,...even a non-human connection--an owl--and it's circular head movement. But at first it wasn't easy for us to see human movement in degrees.We added a number of visual tools: still photos, craft sticks, and moveable paper models. The following video captures some of our thoughts as we explored angles...one
You can grab a free set of the angle lessons by looking for C3 Circles & Angles. What do you do to bring angle measurement to life?
This lesson includes CCSS Standards:
CCSS 4.MD.C.5 Recognize angles as geometric shapes that are formed wherever two rays share a common endpoint, and understand concepts of angle measurement
CCSS 4.MD.C.7 Recognize angle measure as additive. When an angle is decomposed into non-overlapping parts, the angle measure of the whole is the sum of the angle measures of the parts. Solve addition and subtraction problems to find unknown angles on a diagram in real world and mathematical problems, e.g., by using an equation with a symbol for the unknown angle measure.
Credit: Drawings from The Math Learning Center. Used by permission.





incredible post! I learned a lot of new ideas to try. Thanks Cindy!
ReplyDeleteYea! I'm so happy about that!!!
Delete